Il primo prenderà in input una immagine in scala di grigio a 8 bit ed un file contenente una trasformazione nello spazio dei colori rappresentata come 256 valori interi compresi tra 0 e 255. La trasformazione è e tale che l'i-esimo valore di grigio sia mappato nel i-esimo valore di questa sequenza. Il programma applicherà quindi la trasformazione all'immagine scrivendo l'immagine trasformata come output.
Il secondo programma prenderà in input una immagine ed una zona rettangolere della stessa e scriverà in output la trasformazione relativa alla equalizzazione della zona desiderata.
Il terzo programma prenderà due trasformazioni che rappresentano trasformazioni di equalizzazione di due immagini e scriverà in output una trasformazione che porti l'istrogamma della immagine relativa alla prima trasformazione ad essere il più possibile simile all'istogramma della immagine che ha prodotto la seconda trasforamzione.
Una trasformazione prospettica può essere espressa nel seguente modo:
- dato un punto (x,y), lo trasformiamo in coordinate omogenee aggiungendo un 1 in fondo: (x,y,1)
- la trasformazione prospettica in coordinate omogenee viene espressa da una matrice 3x3
![A=[a11, a12, a13; a21, a22, a23; a31, a32, 1]](A.png) .
.
Il punto (x,y,1) diventa quindi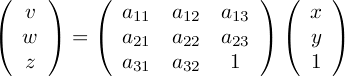 .
. - Il punto viene quindi riportato in coordinate omogenee dividendolo per la terza coordianta (v/z,w/z,1), ottenendo quindi il punto 2D (v/z,w/z).
Rimane il problema di stimare i coefficienti della matrice A. Questo viene fatto risolvendo un sistema lineare nelle otto incognite (a11, a12, a13, a21, a22, a23, a31, a32).
Per questa stima ci servono otto vincoli e quindi quattro coordinate 2D. Assumiamo di voler stimare i coefficienti della trasformazione che porta i punti di coordinate (x11,y11), (x21,y21), (x31,y31), (x41,y41) alle coordinate (x12,y12), (x22,y22), (x32,y32), (x42,y42), questi si ricaveranno dalla soluzione del sistema di equazioni lineari del tipo
per ogni i, [A(xi1,yi1,1)]1=xi2[A(xi1,yi1,1)]3
per ogni i, [A(xi1,yi1,1)]2=yi2[A(xi1,yi1,1)]3
da cui ottengo il sistema lineare
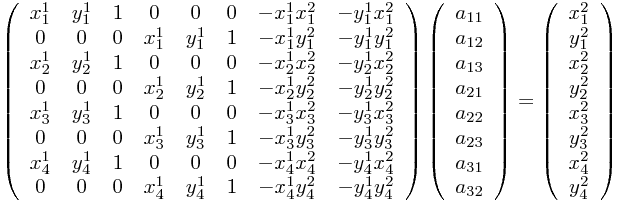
Nota: la maggior parte delle librerie per la FFT richiedono che le dimensioni della immagine siano potenze di 2. dato I estendete ogni dimensione fino alla più piccola potenza di 2 superiore copiando il valore dei pixel più vicini.
[Esempio: immagine trasformata]
Note: Allargate la dimensione della immagine risultante in modo che questa contenga completamente tutte e due le immagini. Per risolvere l'ambiguità tra i punti in comune delle due immagine, date precedenza al colore/valore di una delle due (scegliete voi se la prima o la seconda).